熟年離婚後の安心設計：6つの係数で学ぶ老後資金運用の基本

熟年離婚後の生活を見据える中で、老後の資金計画は非常に重要です。
特に、経済的に独立していく必要がある場合、資産運用の知識は心強い味方となります。
その際に役立つのが「6つの係数」です。これらの係数を活用することで、どのように資金を準備し、効率よく運用するかが見えてきます。
本記事では、老後資金を無理なく賢く準備するために知っておくべき6つの係数を解説し、安心できる老後生活の設計方法を紹介します。

6つの係数とは？老後資金運用に不可欠な知識

6つの係数は、資産計画や運用を計算する際に使われる基本的なツールです。
これらを活用することで、効率的に資産を増やしたり、目標額を無理なく達成したりするための道筋が立てやすくなります。

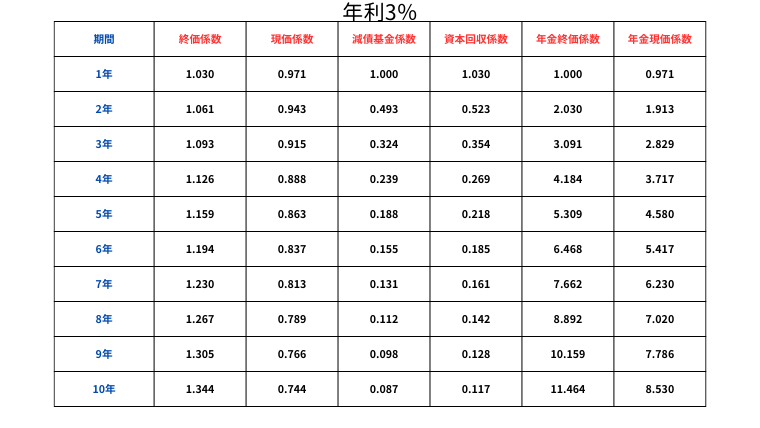
終価係数（しゅうかけいすう）：一括で運用
- 一定の利率で、現在の元本が将来いくらになるかを計算する係数。
- 資産を増やすために投資や貯蓄を行う場合に役立ちます。
  
  例）100万円を年利３％で複利運用した場合、10年後にはいくらになる？
  ＜計算方法＞100万円✕1.344＝134万4千円
現価係数（げんかけいすう）：一括で運用
- 将来の金額が現在の価値に換算するといくらかを計算する係数。
- 老後に必要な資金を現在の価値で把握するのに役立ちます。
  
  例）10年後に100万円にしたい場合、年利３％で複利運用した場合、今いくらあればよい？
  ＜計算方法＞100万円✕0.744＝74万4千円
年金終価係数（ねんきんしゅうかけいすう）：積み立てて運用
- 一定額の積み立てを続けると、将来いくらになるかを計算するための係数。
- 定期的な積立投資やiDeCoなどの資産形成に応用できます。
  
  例）毎年10万円を年利３％で複利運用しながら積み立てた場合、10年後にはいくらになる？
  ＜計算方法＞10万円✕11.464≒114万6千円
減債基金係数（げんさいききんけいすう）：積み立てて運用
- 目標額を積み立てるために、毎年いくらずつ積み立てればよいかを計算するための係数。
- 老後資金を積み立てる計画を立てる際に適しています。
  
  例）10年後に100万円にしたい。年利３％で複利運用した場合、ら毎年いくら積み立てればいい？
  ＜計算方法＞100万円✕0.087＝8万7千円
資本回収係数（しほんかいしゅうけいすう）：取り崩して運用
- 一定の資本を一定期間で取り崩して使う場合、毎年いくら使えるかを計算する係数。
- 老後に年金と退職金を取り崩して生活するシミュレーションに活用できます。
  
  例）100万円を年利３％で複利運用しながら１０年間で取り崩す場合、毎年いくら受け取れる？
  ＜計算方法＞100万円✕0.117＝11万7千円
年金現価係数（ねんきんげんかけいすう）：取り崩して運用
- 将来受け取る年金や定期的な収入の現在価値を計算する係数。
- 退職後の生活費や年金の現価を考える際に使用できます。
  
  例）年利３％で複利運用しながら、毎年１０万円を１０年間受け取るには、今いくらあればよい？
  ＜計算方法＞10万円✕8.530＝85万3千円

社労士ピルエット

福利とは元本だけでなく、それまでに得た利息にも利息がつく仕組みのことです。つまり、利息が利息を生むため、時間が経つほど元本が増え、資産が加速度的に増加します。

資産運用の際の注意点

老後資金の運用では、無理のない計画とリスク管理が重要です。
年利3%という運用利率はあくまで一つの目安であり、実際の運用では市場の変動や経済状況により変わることがあります。
そのため、リスクを分散し、必要に応じて専門家のアドバイスを受けることも検討しましょう。
また、余裕のある資金計画を立てることで、急な出費や予想外の状況にも柔軟に対応できる備えができます。